By Thoralf Mildenberger (ZHAW)
Everybody who knows a bit about R knows that in general loops are said to be evil and should be avoided, both for efficiency reasons and code readability, although one could argue about both.
The usual advice is to use vector operations and apply() and its relatives. sapply(), vapply() and lapply() work by applying a function on each element of a vector or list and return a vector, matrix, array or list of the results. apply() applies a function on one of the dimensions of a matrix or array and returns a vector, matrix or array. These are very useful, but they only work if the function to be applied to the data can be applied to each element independently of each other.
There are cases, however, where we would still use a for loop because the result of applying our operation to an element of the list depends on the results for the previous elements. The R base package provides a function Reduce(), which can come in handy here. Of course it is inspired by functional programming, and actually does something similar to the Reduce step in MapReduce, although it is not inteded for big data applications. Since it seems to be little known even to long-time R users, we will look at a few examples in this post.
The examples are meant to be illustrative and I do not claim that using Reduce() is always the most efficient or clear approach.
The basic idea
Reduce() takes a function f of two arguments and a list or vector x which is to be ‘reduced’ using f. The function is first called on the first two components of x, then with the result of that as the first argument and the third component of x as the second argument, then again with the result of the second step as first argument and the fourth component of x as the second argument etc. The process is continued until all elements of x have been processed. With the accumulate argument we can tell Reduce() to either only return the final result (accumulate == FALSE, the default) or all intermediate results (accumulate == TRUE). There are a few more arguments that can be used to change the order in which x is processed or to provide an initial value, but we won’t use them here.
The help page gives a short description as well as some examples:
?ReduceAs usual with the official help pages, the examples are very condensed and highlight some special features, so we will start with a very easy example here. The cumsum() function returns cumulative sums of a vector:
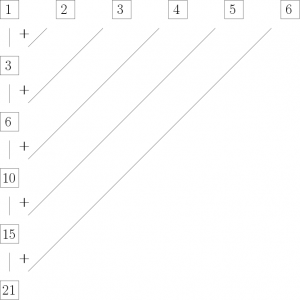
cumsum(1:6)## [1] 1 3 6 10 15 21This can be thought of as applying the function f(a,b) = a + b to the vector x = (1, 2, 3, 4, 5, 6):
y_1 = x_1 = 1
y_2 = x_1 + x_2 = f(x_1, x_2) = 1 + 2 = 3
y_3 = y_2 + x_3 = f(y_2, x_3) = 3 + 3 = 6
y_4 = y_3 + x_4 = f(y_3, x_4) = 6 + 4 = 10
y_5 = y_4 + x_5 = f(y_4, x_5) = 10 + 5 = 15
y_6 = y_5 + x_6 = f(y_5, x_6) = 15 + 6 = 21
or in a more graphical fashion:
This means we can use Reduce()in the following way to produce the same result as cumsum():
Reduce(f = "+", x = 1:6, accumulate = TRUE)## [1] 1 3 6 10 15 21Note that basic arithmetic operators can be called as functions in R when they are quoted:
"+"(1,2)## [1] 31 + 2## [1] 3So we do not have to explicitly define our f function. We also set accumulate = TRUE as accumulate = FALSE only returns the final result:
Reduce(f = "+", x = 1:6, accumulate = FALSE)## [1] 21Example: Joining multiple data frames
A more useful example would be joining multiple data frames with the same ids but different other columns. While there is a ready-made function join_all() for this in the plyr package, we will see shortly how to solve this task using Reduce() using the merge() function from base R.
Suppose we have a couple of data frames each containing different information about customers of an online shop. They all have a common ID column Customer_ID, and we want to join them into one big table.
df1 <- data.frame(Customer_ID = c(1, 2, 3), Name = c("John", "Sue", "Ann"))
df2 <- data.frame(Customer_ID = c(1, 3), Year_First_Order = c(2011, 2017))
df3 <- data.frame(Customer_ID = c(1, 2, 3),
Date_Last_Order = c("2017-03-03", "2014-03-01", "2017-05-30"),
No_Items_Last_Order = c(3, 1, 1),
Total_Amount_Last_Order = c(49, 25,25))
df4 <- data.frame(Customer_ID = c(2, 3), Interested_In_Promo = c(TRUE, FALSE))We could do so by first joining the first two data frames, then join the result with the third, and then join the results of that with the fourth table:
df_merge <- merge(df1, df2, by = "Customer_ID", all.x = TRUE, all.y = FALSE)
df_merge <- merge(df_merge, df3, by = "Customer_ID", all.x = TRUE, all.y = FALSE)
df_merge <- merge(df_merge, df4, by = "Customer_ID", all.x = TRUE, all.y = FALSE)
df_merge## Customer_ID Name Year_First_Order Date_Last_Order No_Items_Last_Order
## 1 1 John 2011 2017-03-03 3
## 2 2 Sue NA 2014-03-01 1
## 3 3 Ann 2017 2017-05-30 1
## Total_Amount_Last_Order Interested_In_Promo
## 1 49 NA
## 2 25 TRUE
## 3 25 FALSEWe could also store all the data frames in one list and then use merge() with the appropriate arguments as our f function:
df_list <- list(df1, df2, df3, df4)
Reduce(function(d1, d2) merge(d1, d2, by = "Customer_ID", all.x = TRUE, all.y = FALSE),
df_list)## Customer_ID Name Year_First_Order Date_Last_Order No_Items_Last_Order
## 1 1 John 2011 2017-03-03 3
## 2 2 Sue NA 2014-03-01 1
## 3 3 Ann 2017 2017-05-30 1
## Total_Amount_Last_Order Interested_In_Promo
## 1 49 NA
## 2 25 TRUE
## 3 25 FALSEExample: Sums of matrix powers
We can also combine lapply() and Reduce(), like in the following example. Given a markov chain with transition matrix P
P <- rbind(c(0.9, 0.1), c(1, 0))
P## [,1] [,2]
## [1,] 0.9 0.1
## [2,] 1.0 0.0the matrix M(K) defined by
M(K) = I + P + P^2 + P^3 + … + P^K
has the following interpretation: Component (M(K))_ij gives the expected number of time steps the chain stays in state j when starting in state i. Give a matrix P one can of course calculate M(K) using a loop, but we do it differently. We first create a list of matrix powers (using the matrix power function from the expm package):
library(expm)
P_powers <- lapply(0:20, function(k) P %^% k)
head(P_powers)## [[1]]
## [,1] [,2]
## [1,] 1 0
## [2,] 0 1
##
## [[2]]
## [,1] [,2]
## [1,] 0.9 0.1
## [2,] 1.0 0.0
##
## [[3]]
## [,1] [,2]
## [1,] 0.91 0.09
## [2,] 0.90 0.10
##
## [[4]]
## [,1] [,2]
## [1,] 0.909 0.091
## [2,] 0.910 0.090
We could first think of using sum(). sum() does not work with lists, and unlisting does not give the desired result, as instead of a matrix the sum of all components of matrix powers is returned:
sum(unlist(P_powers))## [1] 42But we can use Reduce() with "+", as this correctly adds the matrices componentwise:
Reduce("+", P_powers)## [,1] [,2]
## [1,] 19.17355 1.826446
## [2,] 18.26446 2.735537One potential drawback compared to using a loop is that we store the whole list of matrix powers, although each power is used only once.
Example: Simulating a trajectory of a Markov Chain without a loop
The next one is a bit hacky but fun: We want to simulate a trajectory from a Markov chain. Suppose we are given the transition matrix, the starting state, and the number of steps to simulate:
P <- matrix(c(0, 0.1, 0.9, 0.2, 0.5, 0.3, 0, 0.5, 0.5), ncol = 3, byrow = T);
P## [,1] [,2] [,3]
## [1,] 0.0 0.1 0.9
## [2,] 0.2 0.5 0.3
## [3,] 0.0 0.5 0.5x_0 <- 2
K <- 100000The idea is the following: We can simulate the next state of the Markov Chain given the current state and a random number from a uniform distribution on [0,1]:
newstate <- function(oldstate,u) {
which.min(u>cumsum(P[oldstate,]))
}
x_1 <- newstate(x_0, runif(1))
x_1## [1] 1We get the probabilities for the next state from the row of P that is given by the number of the current state, and we can sample from the states by using comparing a uniform random number to the cumulative sum of the probabilities (this amounts to inverting the cumulative distribution function of the next state give the current one).
Of course, we can use the function newstate() on the result and a new random number:
x_2 <- newstate(x_1, runif(1))
x_2## [1] 3So we could use newstate() in Reduce(). The only problem is that it takes arguments of different type: The first one is an integer giving the current state, the second one is a real number. Since the integer can be coerced to double, Reduce() still works here. We just have to provide a vector that contains the starting state as first component and the K uniform random numbers needed to generate the following states. We also set accumulate = TRUE, because we want the whole trajectory and not only the state at time K:
mc_without_loop <- Reduce(newstate, c(x_0, runif(K)), accumulate = TRUE)
head(mc_without_loop)## [1] 2 2 3 2 2 2# Distribution of states:
table(mc_without_loop)/length(mc_without_loop)## mc_without_loop
## 1 2 3
## 0.09183908 0.46318537 0.44497555Further reading
The Reduce() function is relatively sparsely documented and seems to be widely unknown. It is also often not treated in books on programming in R, even in more advanced ones. Some useful references are
- The official help page (
?Reduce) - Headly Wickham’s book Advanced R is available online at http://adv-r.had.co.nz/ and the chapter on functional programming contains a short section on
Reduce(). - Follow-up post on some pitfalls using reduce()
Your explanation is excellent and helpful. Thanks a lot.
Thanks for the useful illustrations. I also came across Reduce() for the first time after many years of R experience. I use it in Taylor Series approximations for matrix exponentials such as e^W where W is a matrix.
how could I get the reduce package?
You do not even need a package. It’s a built-in function, which makes it even more remarkable that it is very widely unknown. Just Type ?Reduce for the help page.